Se ho un segnale da campionare la cui frequenza è F, qual è la sample rate minima che posso utilizzare per il campionamento di quel segnale, senza incappare in una serie di fenomeni tali da distorcere il segnale? Consideriamo un semplice segnale periodico puro (un suono sinusoidale). Ogni ciclo di oscillazione si compone di una fase positiva e di una negativa e pertanto per campionare questa alternanza mi occorrono almeno due campioni.

Il teorema di H. Nyquist (detto del campionamento), formulato nel 1928, afferma che considerato un segnale di frequenza F, lo si può campionare a patto che si utilizzi una sample rate che sia almeno il doppio di F.

SR ≥2F

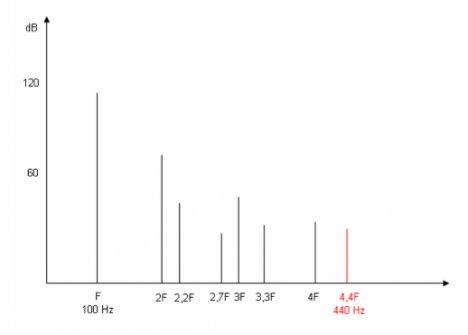
Nel caso però che il segnale da campionare sia periodico complesso, ovvero costituito da numerose componenti sinusoidali (parziali armoniche e non armoniche), come nell'immagine di questo post, che riproduce lo spettro acustico di un simile segnale, occorre stabilire quale sia la F del segnale da prendere in considerazione. In questo caso bisogna considerare la parziale con frequenza maggiore in quanto è quella che più velocemente alterna l’oscillazione sinusoidale tra la fase positiva e quella negativa. Nella figura la parziale in questione è stata colorata di rosso e pertanto è F = 440 Hz: ciò significa che per campionare questo segnale dovrò utilizzare una sample rate almeno pari a 880 Hz. In tal caso la formulazione del teorema di Nyquist è la seguente: considerato un segnale audio, lo si può campionare a patto che si utilizzi una sample rate che sia almeno il doppio della frequenza F relativa alla componente sinusoidale più elevata presente nello spettro acustico.

S ≥2F(Max)

Questo però significa che il segnale da campionare deve avere una componente più acuta nello spettro individuabile ovvero che deve essere limitato nella banda acustica. Tutte le componenti di frequenza superiore devono essere eliminate dallo spettro. Siamo ora in grado di formulare pienamente il teorema del campionamento: preso un segnale audio limitato in banda, per campionarlo occorre utilizzare una sample rate che sia almeno il doppio della frequenza F relativa alla componente sinusoidale più acuta presente nello spettro acustico del segnale.

Soffermiamoci un attimo: la banda del segnale deve essere limitata ossia deve esserci una frequenza massima all'interno del segnale che non deve mai essere superata. Poi, misurata questa frequenza massima, il teorema afferma che la sample rate da utilizzare deve essere almeno doppia di questa frequenza massima perchè il campionamento possa essere realizzato con successo. Ad esempio: se vogliamo campionare un segnale audio la cui frequenza massima sia, per ipotesi, 300Hz (ovvero l'onda sonora più "veloce" compie 300 cicli al secondo), la sample rate dovrà essere come minimo di 600Hz, ossia dovranno essere presi almeno 600 campioni in un secondo. Se però dobbiamo campionare un segnale che arrivi, ad esempio, fino a 15.000 Hz, sarà necessaria una frequenza di campionamento di almeno 30.000Hz, ossia si dovranno prendere almeno 30.000 misurazioni al secondo. Nella pratica, in ragione del fatto che lo spettro udibile è compreso tra i 20 e i 20.000Hz, sarebbe sufficiente prendere una sample rate di 40.000Hz per campionare ogni possibile suono udibile dall'uomo.

Ciò che avviene nella digitalizzazione rispetta il teorema del campionamento procedendo in senso inverso. Stabilito un tasso di campionamento SR, occorre eliminare dal segnale tutte quelle frequenze che sono oltre la metà di SR; quindi, se SR = 11.000 campioni al secondo, occorre eliminare dal segnale tutte le frequenze superiori a 5500 Hz. Per far ciò si utilizza un filtro passabasso che elimina (o meglio attenua) tutte le frequenze sopra quella di riferimento (detta frequenza di taglio o di cutoff). Ovviamente tale filtro è detto passabasso (LP, lowpass filter) in quanto fa “passare” solamente le frequenze sotto la frequenza di taglio, ed è detto di antialiasing in quanto evita il fenomeno dell’aliasing, noto anche come foldover. Quindi, prima di campionare il segnale occorre filtrarlo in modo da eliminare una parte del suo spettro che potrebbe causare il problema dell’aliasing (argomento del prossimo post)